Principis de conservació
Una de les conquistes més importants del saber humà ha estat el descobriment de magnituds físiques que romanen constants durant l’evolució d’un sistema físic. Quan trobem una magnitud que no canvia mentre un sistema evoluciona imposa límits sobre aquest procés i ens proporciona eines matemàtiques que ens permeten descriure aquesta evolució de manera que d’una altra forma seria impossible o molt més difícil de fer.
Quan tenim una magnitud que roman constant durant l’evolució d’un sistema direm que la magnitud es conserva, que es conservativa o que és un invariant. El nom de principi de conservació té origen històric, actualment resulta més correcte dir que es tracta de teoremes de conservació, ja que aquestes lleis de conservació es poden deduir de les lleis del moviment que adoptem com principis, com ser les lleis de Newton de la dinàmica.
Una característica molt important de les magnituds que es conserven és que cadascuna d’elles està associada a alguna simetria del sistema. Avui sabem que si descobrim una simetria en un sistema físic, hi haurà una magnitud física que es conservarà. Aquesta aproximació ha estat molt exitosa en la física moderna.
Conservació de la quantitat de moviment
Quantitat de moviment o moment lineal
Ja hem vist que si coneixem les forces implicades en una interacció, a partir de les equacions de Newton podem determinar les acceleracions dels cossos implicats i predir l’evolució del sistema trobant les seves posicions en funció del temps. Moltes vegades les interaccions són massa complexes o no coneixem com són les forces implicades, aleshores no podem utilitzar les equacions de Newton per predir l’evolució del sistema. Però, potser podem definir noves magnituds físiques amb les que podríem predir algunes coses sobre l’evolució dels sistemes. La primera magnitud que definirem serà la quantitat de moviment, moment lineal o momentum:
\[\vec{p}=m\vec{v}\]És una magnitud vectorial que té la mateixa direcció i sentit que la velocitat i les seves unitats són \(\mathrm{kgm/s}\) en el SI.
Teorema de l’impuls i la quantitat de moviment
La quantitat de moviment està relacionat amb les forces aplicades sobre un cos. Podem reescriure la segona llei de Newton de la següent manera:
\[\sum_{i}\vec{F_{i}}=m\vec{a}=m\frac{\Delta\vec{v}}{\Delta t}=\frac{m(\vec{v}-\vec{v}_{0})}{\Delta t}=\frac{m\vec{v}-m\vec{v}_{0}}{\Delta t}=\frac{\vec{p}-\vec{p}_{0}}{\Delta t}=\frac{\Delta\vec{p}}{\Delta t}\]L’última relació es pot reescriure de la següent manera:
\[\left(\sum_{i}\vec{F_{i}}\right)\Delta t=\Delta\vec{p}\]És a dir, la força neta sobre el sistema multiplicat pel temps d’actuació d’aquesta força neta, resulta igual a la variació de la quantitat de moviment.
Aprofitarem per definir ara altra magnitud física, l’impuls mecànic, \(\vec{I}\),
\[\vec{I}=\left(\sum_{i}\vec{F_{i}}\right)\Delta t=\vec{F}\Delta t\]Les unitats de l’impuls són \(\mathrm{Ns}\) en el SI.
En la figura de sota es pot veure la gràfica de la força en funció del temps en el cas d’una força constant. En aquest cas es pot veure clarament que l’impuls es pot interpretar com l’àrea sota dintre de la gràfica (zona grisa).
La interpretació anterior es pot generalitzar en el cas que la força no fos constant, com és el cas de la figura següent. En aquest cas sempre podem subdividir l’àrea en petites regions on la força roman constant i calcular l’impuls com la suma de totes aquestes àrees petites. D’aquesta manera veiem que la interpretació de l’àrea sota la gràfica com l’impuls és completament general i no només per a casos de força constant.
Amb la definició d’impuls que hem adoptat podem enunciar el teorema de l’impuls mecànic i la quantitat de moviment com:
\[\Delta\vec{p}=\vec{I}\]Un corol·lari important d’aquest teorema ens diu que si el sistema no rep cap força neta (\(\vec{F}=0\)), aleshores l’increment de quantitat de moviment resulta nul, això vol dir que la quantitat de moviment roman constant, en aquests casos diem que la quantitat de moviment es conserva.
\[\Delta\vec{p}=\vec{p}-\vec{p}_{0}=0\]o, equivalentment,
\[\vec{p}=\vec{p}_{0}\]El cas de dos partícules que interactuen de manera aïllada és un cas particular d’aplicació d’aquest corol·lari. Imaginem dos partícules que es mouen sobre una superfície plana, xoquen entre elles i continuen amb trajectòries diferents. En aquest cas les forces que actuen son les forces que es fan una partícula a l’altra i viceversa. Les dues forces formen un parell d’interacció i, per tant, són iguals i contraries i la seva suma resulta nul·la.
Si considerem les dues partícules alhora com un únic sistema, l’impuls total d’aquest sistema resultarà nul i la quantitat de moviment total del sistema romandrà constant durant tot el procés, independentment de les característiques que tingui la interacció entre elles. Hem trobat una constant de moviment!
\[\vec{p'}=\vec{p}\] \[\vec{p_{1}'}+\vec{p_{2}'}=\vec{p_{1}}+\vec{p_{2}}\] \[m_{1}\vec{v}'_{1}+m_{2}\vec{v}'_{2}=m_{1}\vec{v}_{1}+m_{2}\vec{v}_{2}\]Veurem com aquest teorema de conservació juntament amb el de conservació de l’energia ens permetrà resoldre problemes de relativa alta complexitat.
Conservació de l’energia
Energia
Probablement el d’energia sigui el concepte més important de la ciència. Tot l’univers està format només d’energia, el que passa és que es manifesta de diferents maneres. Quan parlem de matèria també estem parlant d’energia, avui sabem que la matèria és energia encapsulada i, gràcies a la famosa equació d’Einstein, \(E=mc^{2}\), coneixem la seva equivalència. L’energia es manifesta en moltes altres formes, però que són més intangibles que la matèria, com ser el moviment, la compressió d’una molla, les ones electromagnètiques, la energia associada a l’atracció gravitatòria, etc.
Per aquest motiu el concepte d’energia resulta més abstracte i difícil d’entendre, ja que l’energia no només pot ser una cosa, sinó també un procés, com si fos un substantiu i un verb alhora. Les coses tenen energia però on nosaltres no la veiem i només ens adonem de la seva existència quan aquesta es transforma o es transfereix. Quan ens freguem les mans, aquest moviment és una forma d’energia, i nosaltres sentim com les nostres mans comencen a escalfar-se. Aquest és un exemple de transformació de l’energia, on l’energia del moviment de les nostres mans es transforma en energia tèrmica que fa pujar la temperatura de les nostres mans. Els processos de transformació es troben a tot arreu a la natura, nosaltres, per exemple, obtenim l’energia per viure a través de la digestió dels aliments. En aquesta unitat estudiarem aquest concepte, sobre tot, limitat a l’estudi del moviment. Per començar definirem un concepte relacionat amb l’energia, el concepte de treball.
Treball
Veurem com el concepte d’energia està relacionat amb el concepte de treball d’una força. Abans de veure aquesta relació però, haurem de definir el treball. Si considerem el cas d’una força constant, \(\vec{F}\), que actua sobre un cos, i aquest es desplaça produint un vector desplaçament, \(\Delta\vec{r}\), direm que el treball, W, produït per la força sobre el cos resulta igual al producte escalar del vector força per el vector desplaçament
\[W=\vec{F}·\Delta\vec{r}\]Com ho diu el seu nom el resultat d’aquest producte escalar és una magnitud escalar, i les seves unitats de mesura són newton \(\times\) metre, que rep el nom de joule \((1\mathrm{Nm=1J})\) en el Sistema Internacional.
Per a fer el càlcul del treball utilitzarem la definició de producte escalar, que resulta igual a la multiplicació dels mòduls dels vectors multiplicats pel cosinus de l’angle format entre ells, així,
\[W=\left|\vec{F}\right|\left|\Delta\vec{r}\right|\cos\alpha\]És important destacar que aquesta definició de treball serveix per a una força constant. En la figura següent es veu una situació on la força forma un angle \(\alpha\) amb el desplaçament.
.
És important destacar que una força no realitza treball si la seva direcció és perpendicular al desplaçament, ja que en aquest cas l’angle és \(\alpha=90^{\circ}\) i \(\cos(90^{\circ})=0\).
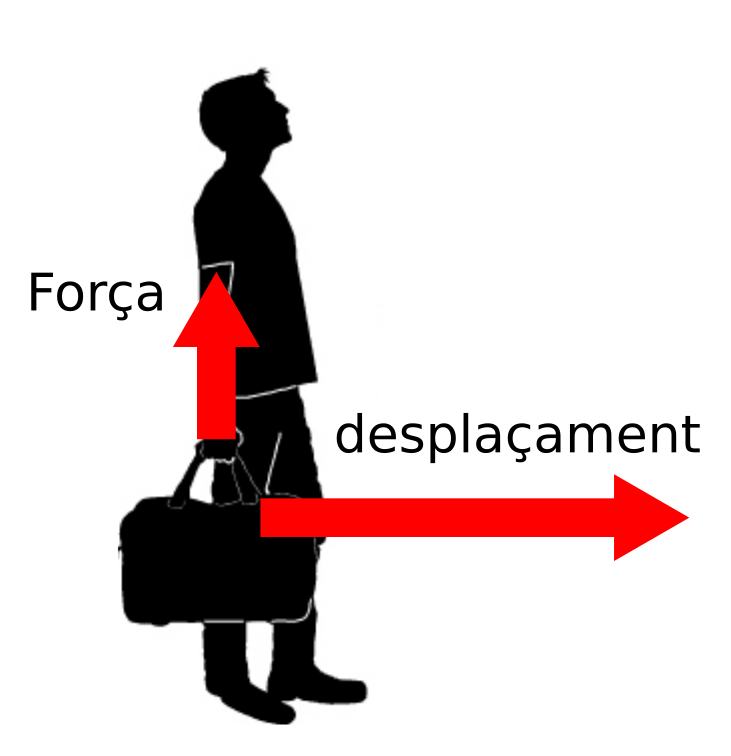
A la figura inferior es veu un home que porta una maleta a la ma, si es desplaça a velocitat constant, l’única força que ha de fer és la necessària per a equilibrar el pes de la maleta, per tant, essent la força perpendicular al desplaçament, l’home no fa treball en el sentit que li dona la física a aquest concepte, però, això no vol dir que no hagi de fer un esforç físic per desplaçar la maleta. En aquest exemple es veu com moltes vegades, els conceptes físics no coincideixen amb la utilització popular dels termes. Amb el concepte d’energia també hi ha molts malentesos.
Considerem una força constant, de mòdul \(F\), que produeix un desplaçament, de mòdul \(\Delta x\), en la mateixa direcció i sentit que la força. En aquest cas el treball resulta igual a
\[W=F\Delta x\]ja que l’angle format entre la força i el vector desplaçament es zero i, el seu cosinus és igual a 1. A la gràfica de la figura de sota tenim un exemple en el qual hi ha una força de 2 N paral·lela a la direcció del desplaçament que actua sobre un cos i produeix un moviment que fa que el cos passi de la posició \(x=2\,\mathrm{m}\) a la posició \(x=8\,\mathrm{m}\), produint un desplaçament \(\Delta x=6\,\mathrm{m}\).
El treball resulta igual a \(W=12\,\mathrm{J}\). El valor del treball resulta igual a l’àrea que hi ha sota la gràfica de la força. Aquesta interpretació del treball com l’àrea sota la gràfica de força-posició resulta completament general i la podem utilitzar per fer el càlcul de treball de forces que no siguin constants.
Energia cinètica
Considerem un cos que està sotmès a una força total constant, en aquest cas el cos experimenta un moviment rectilini uniformement accelerat i resulta vàlida la següent relació,
\[v^{2}-v_{0}^{2}=2a\Delta x\]Si multipliquem ambdues bandes de la relació anterior per la massa del cos i dividim per 2 ens queda:
\[\frac{1}{2}mv^{2}-\frac{1}{2}mv_{0}^{2}=ma\Delta x\]Per la segona llei de Newton sabem que \(F=ma\), per tant, a la banda de la dreta de l’equació tenim el treball de la força neta aplicada sobre el cos i a la banda esquerra hi ha la diferència d’una expressió, \(\frac{1}{2}mv^{2}\), relacionada amb l’estat de moviment del cos entre l’estat final i inicial. Anomenarem a aquesta expressió energia cinètica, \(E_{c}\):
\[E_{c}=\frac{1}{2}mv^{2}\]De manera que el treball total efectuat sobre el cos resulta igual a la diferència d’energia cinètica entre l’estat final i inicial,
\[W_{T}=E_{c}(\mathrm{final})-E_{c}(\mathrm{inicial})\] \[W_{T}=\Delta E_{c}\]Aquesta igualtat es coneix com el teorema del treball i l’energia cinètica.
És important notar que pel treball es compleix el principi de superposició, es a dir, el treball de la suma de forces aplicades sobre un cos resulta igual a la suma dels treballs individuals de totes les forces aplicades.
Energia potencial
Hi ha interaccions que permeten als objectes emmagatzemar energia degut a la seva posició respecte a altre objecte. Aquesta energia emmagatzemada es diu energia potencial, degut a que l’objecte que la conté té el potencial de realitzar treball a càrrec de la seva energia potencial.
Energia potencial gravitatòria
Un exemple d’energia potencial és la gravitatòria, un objecte elevat (separat de la Terra) té el potencial de realitzar treball, ja que si deixem lliure l’objecte, comença a apropar-se a la terra degut a la seva força pes, realitzant treball.
Calculem el treball realitzat per la força pes sobre un cos de massa m en dos supòsits, en el primer cas baixant amb caiguda lliure, des d’una altura \(h_{0}\) fins a arribar a una altura \(h_{f}\), el treball resulta igual a:
\[W=\vec{P}.\Delta\vec{r}=-mg\Delta h=-\left[mgh_{f}-mgh_{0}\right]\]on \(g\) correspon al mòdul de l’acceleració de la gravetat. El treball resulta positiu, ja que \(h_{f}<h_{0}\).
A la figura inferior es pot veure el primer cas a l’esquerra i a la dreta tenim el segon cas, on el cos baixa per un pla inclinat d’angle \(\beta\). El treball el podem calcular com,
\[W=\vec{P}.\Delta\vec{r}=mg\left|\Delta\vec{r}\right|\cos(\alpha)=mg\left|\Delta h\right|=-mg\Delta h=-\left[mgh_{f}-mgh_{0}\right]\]on hem utilitzat que \(\mid\Delta\vec{r}\mid\cos(\alpha)=\mid\Delta h\mid\).
Podem confirmar que el resultat és coincident en ambdós casos i generalitzar que el treball de la força pes no depèn del camí sinó només de la diferència d’altura. Quan el treball d’una força no depèn del camí sinó només de les posicions inicial i final podem definir una funció anomenada energia potencial, la diferència de la qual avaluada entre la posició inicial i final, ens dona el treball realitzat per la força.
D’aquesta manera definim energia potencial gravitatòria o energia potencial gravitacional com
\[U_{g}=mgh\]de manera que el treball de la força pes resulta
\[W=-\left(U_{g}(\text{final})-U_{g}(\text{inicial})\right)=-\Delta U_{g}\]Dir que el treball de la força pes no depèn del camí és equivalent a dir que el treball de la força pes al llarg d’un camí tancat és igual a zero. Això es pot veure a la figura inferior, si el cos va pel camí 1 el treball de la força pes resulta
\[W_{AB}=U_{A}-U_{B}\]i si ara torna pel camí 2 tenim que el treball resulta
\[W_{BA}=U_{B}-U_{A}\]El treball anant pel camí 1 i tornant pel camí 2 (camí tancat) aleshores resulta nul
\[W_{ABA}=W_{AB}+W_{BA}=U_{A}-U_{B}+U_{B}-U_{A}=0\]
Energia potencial elàstica
L’energia potencial gravitatòria no és pas l’única interacció per a la qual podem definir una energia potencial. La força elàstica també té la característica de que el treball que realitza només depèn de les posicions inicial i final. A la figura següent podem veure com varia la força elàstica en funció de la posició. Considerem el cas d’un cos lligat a una molla i volem calcular el treball fet per la força elàstica sobre el cos quan el cos es mou des de la posició \(x_{0}\) fins a la posició \(x\). La força elàstica segueix la llei d’Hooke \((F_{e}=-kx)\), es a dir, resulta proporcional a l’apartament respecte de la posició d’equilibri que s’obté quan la molla es troba amb la seva longitud lliure.
El treball de la força elàstica es pot obtenir calculant l’àrea indicada a la gràfica de la figura següent. Per fer el càlcul podem calcular l’àrea del triangle amb vèrtexs \((0,x,-kx)\) i restar-li la del triangle de vèrtexs \((0,x_{0},-kx_{0})\):
\[W=\left(\frac{-kx.x}{2}\right)-\left(\frac{-kx_{0}.x_{0}}{2}\right)=-\left(\frac{1}{2}kx^{2}-\frac{1}{2}kx_{0}^{2}\right)\]Queda palès que el treball de la força elàstica només depèn de la posició inicial i final. Seguint el mateix raonament que per a la força gravitatòria podem definir una energia potencial elàstica com
\[U_{e}=\frac{1}{2}kx^{2}\]Amb aquesta definició resulta que el treball de la força elàstica és igual a
\[W=-\left(U_{e}(\text{final})-U_{e}(inicial)\right)=-\Delta U_{e}\]La conservació de l’energia
Hem vist que hi ha algunes interaccions per a les quals es poden definir unes funcions anomenades energies potencials. L’hem vist pel cas de la interacció gravitatòria i de l’elàstica, n’hi ha d’altres i les veurem més endavant. Aquest tipus d’interaccions tenen una gran importància i es coneixen com interaccions conservatives o forces conservatives i a continuació investigarem el perquè d’aquesta denominació.
Dividirem les forces en dos conjunts, el conjunt de les forces per a les que el treball no depèn del camí i per a les quals podem definir una energia potencial, que anomenarem forces conservatives, i la resta, que anomenarem forces no conservatives o forces dissipatives.
Més amunt hem deduït el teorema del treball i l’energia cinètica, que deia que el treball de la suma de totes les forces és igual a l’increment de l’energia cinètica:
\[W(\text{totes})=\Delta E_{c}\]Ara també podem establir que el treball de les forces conservatives és igual a l’increment de l’energia potencial canviat de signe:
\[W(\text{conservatives})=-\Delta U\]Si restem membre a membre ambdues equacions tenim:
\[W(\text{no conservatives})=W(\text{totes})-W(\text{conservatives})=\Delta E_{c}+\Delta U\]Si definim energia mecànica com la suma d’energia potencial més energia potencial, tenim:
\[E_{M}=E_{c}+U=\frac{1}{2}mv^{2}+U\]on l’energia potencial correspon a la suma de totes les energies potencials que corresponguin. Amb aquesta definició arribem al teorema de conservació de l’energia mecànica, ja que si totes les forces que atuen sobre un sistema són conservatives, el treball de les forces no conservatives és nul i així també la variació de l’energia mecànica. Per tant, si les forces que actuen són totes conservatives (o si hi ha de no conservatives, no fan treball perquè són perpendiculars al desplaçament com la forces de contatcte, per exemple), l’energia mecànica és una constant de moviment, es conserva:
\[\Delta E_{M}=0\]Quan parlem de forces no conservatives o dissipatives volem dir que són forces que no conserven l’energia mecànica però això no vol dir que si comptabilitzem totes les altres formes possibles d’energia l’energia no es conservi. Per exemple, si considerem el moviment d’un cos sobre el terra, veurem que després de recórrer una certa distància acaba aturant-se. Això passa perquè sobre el cos actua una força dissipativa, la força de fregament, que fa que l’energia mecànica no es conservi. On ha anat a parar aquesta energia? Va desaparèixer? En realitat no, el que passa en aquest cas és que l’energia mecànica que es perd, en realitat es transforma en energia tèrmica que es transfereix al medi i al mateix cos. Aquesta energia térmica el que fa és agitar més violentament les molècules que formen part del cos i el medi al seu voltant que acaben movent-se amb més velocitat, per tant, a nivell microscòpic l’energia tèrmica és l’energia cinètica de les partícules que formen la matèria. Per tant, si comptabilitzem totes les formes d’energia podem dir que l’energia sempre es conserva.
Forces dissipatives
Quan vam trobar les forces conservatives, vam veure que una característica fonamental d’aquestes forces és que el treball que fan quan recórren un camí tancat resulta nul. Podem veure que el treball que fa la força de fregament quan recórre un camí tancat resulta no nul. Considerem un cos que es mou cap a la dreta fregant amb el terra, la força de fregament s’oposarà al lliscament de superfícies i per tant tindrà sentit contrari al desplaçament i el treball resultant serà negatiu. Si ara fem que el cos desfaci el seu camí tornant enrrere, el desplaçament canviarà de sentit però també ho farà la força, de manera que el treball tornarà a ser negatiu i el resultat al cap de fer un camí tancat no resultarà nul.
Xocs
Considerarem un xoc o col·lisió com una interacció entre dos o més cossos o partícules en la qual no necessàriament ha d’haver contacte material i al menys una de les partícules està en moviment. Si considerem com sistema totes les partícules que participen en el xoc, com totes les forces que hi ha són interaccions internes del sistema, la suma total de forces resulta nul·la, ja que a cada força li correspon el seu parell d’interacció dintre del sistema (3a llei de Newton). Si tenim en compte el teorema de l’impuls i la quantitat de moviment, l’impuls total del sistema resulta nul degut a que la força neta és nul·la i aleshores la quantitat de moviment es conserva per a tot el sistema.
Xoc elàstic
El xoc elàstic és un procés en el qual a més de conservar-se la quantitat del moviment es conserva l’energia cinètica del sistema. Aquest tipus de xocs es donen a la física de partícules subatòmiques i amb certa aproximació en processos macroscòpics com per exemple el xoc de boles de billar.
Considerem dues partícules de masses \(m_{1}\) i \(m_{2}\) que es mouen amb velocitats \(\vec{v}_{1}\) i \(\vec{v}_{2}\) respectivament. Després de xocar les partícules tenen velocitat \(\vec{v}^{,}_{1}\) i \(\vec{v}^{,}_{2}\). Suposarem que les velocitats després del xoc són desconegudes i intentarem trobar-les. Per raons de simplicitat considerarem que el moviment és unidimensional tal com mostra la figura de sota.
La conservació de la quantitat de moviment pel sistema ens porta a la relació
\[p^{,}=p\] \[\begin{equation}\label{eq:cons_p} m_{1}v_{1}^{,}+m_{2}v{}_{2}^{,}=m_{1}v{}_{1}+m_{2}v{}_{2} \end{equation}\]que ens diu que la quantitat de moviment del conjunt format per les dues partícules és igual abans i després del xoc. L’equació anterior la podem reescriure de la manera
\[\begin{equation}\label{eq:cons_p_2} m_{1}\left(v_{1}^{,}-v_{1}\right)=m_{2}\left(v_{2}-v{}_{2}^{,}\right) \end{equation}\]Aquesta expressió la utilitzarem més endavant.
La conservació de l’energia cinètica ens dona la següent equació
\[E'_{c}=E_{c}\] \[\frac{1}{2}m_{1}v_{1}^{,2}+\frac{1}{2}m_{2}v{}_{2}^{,2}=\frac{1}{2}m_{1}v{}_{1}^{2}+\frac{1}{2}m_{2}v{}_{2}^{2}\]El factor 1/2 apareix a totes dues bandes de l’equació i els podem eliminar multiplicant ambdues bandes de l’equació per 2. Si després reagrupem el termes podem tenir
\[m_{1}v{}_{1}^{,2}-m_{1}v{}_{1}^{2}=m_{2}v{}_{2}^{2}-m_{2}v{}_{2}^{,2}\]i, traient les masses com factor comú obtenim
\[m_{1}\left(v_{1}^{,2}-v{}_{1}^{2}\right)=m_{2}\left(v_{2}^{2}-v{}_{2}^{,2}\right)\]i encara podem factoritzar les diferències de quadrats (producte notable)
\[m_{1}\left(v_{1}^{,}-v_{1}\right)\left(v_{1}^{,}+v_{1}\right)=m_{2}\left(v_{2}-v{}_{2}^{,}\right)\left(v_{2}+v{}_{2}^{,}\right)\]Però, degut a l’equació \(\eqref{eq:cons_p_2}\), dividint membre a membre l’equació \(\eqref{eq:cons_p}\) obtenim:
\[\begin{equation}\label{eq:xoc_elast} v_{1}^{,}+v_{1}=v_{2}+v{}_{2}^{,} \end{equation}\]Les equacions \(\eqref{eq:cons_p}\) i \(\eqref{eq:xoc_elast}\) conformen un sistema de dues equacions lineals amb dues incògnites que permeten obtenir les velocitats de les partícules just després del xoc. Com no hem fet cap hipòtesi quant als valors de les velocitats, aquests resultats són totalment generals per a xocs elàstics unidimensionals.
Xoc plàstic
El xoc plàstic o perfectament inelàstic és un xoc en el qual les dues partícules queden enganxades després del xoc. En aquest cas també es conserva la quantitat de moviment del sistema però no hi ha conservació de l’energia, part de la qual es perd durant el xoc.
Coneixent les masses i velocitats abans del xoc podem obtenir la velocitat del cossos després del xoc només plantejant la conservació de la quantitat de moviment:
\[(m_{1}+m_{2})v^{,}=m_{1}v_{1}+m_{2}v_{2}on v^{,}\]és la velocitat del conjunt després del xoc, d’aquí obtenim la velocitat del conjunt després del xoc:
\[v^{,}=\frac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}\]Xoc parcialment inelàstic
Entre els dos casos explicats anteriorment trobem els xocs que no són elàstics ni plàstics, són xocs en els que es conserva la quantitat de moviment però no l’energia cinètica com en el cas dels xocs plàstics però no queden enganxats, per tant hi ha dues velocitats, \(v_{1}^{,}\) i \(v_{2}^{,}\), després del xoc però només hi ha una llei de conservació, per tant, hem de tenir dades sobre la velocitat d’un dels cossos per a poder trobar la velocitat de l’altre. També podem trobar les velocitats si coneixem el valor de la pèrdua d’energia en el xoc.
Explosions
El cas d’una explosió es pot interpretar com el d’un xoc plàstic però invertit en el temps. Considerem el cas d’una granada, inicialment tenim un cos i després de l’explosió tots els fragments de la granada surten volant. Com el procés de l’explosió és intern de la granada, totes les forces són internes i la quantitat de moviment es conserva en aquest procés. En canvi, l’energia mecànica no és conserva, ja que hi ha un increment important de l’energia mecànica. D’on surt aquesta energia?, doncs de l’energia interna emmagatzemada a la granada en forma d’energia potencial química.
