Moviment

La filosofia è scritta in questo grandissimo libro, che continuamente ci sta aperto innanzi agli occhi (io dico l’ Universo’), ma non si può intendere, se prima non il sapere a intender la lingua, e conoscer i caratteri ne quali è scritto. Egli è scritto in lingua matematica, e i caratteri son triangoli, cerchi ed altre figure geometriche, senza i quali mezzi è impossibile intenderne umanamente parola; senza questi è un aggirarsi vanamente per un oscuro labirinto.

Galileu

I often say that when you can measure what you are speaking about, and express it in numbers, you know something about it; but when you cannot measure it, when you cannot express it in numbers, your knowledge is of a meagre and unsatisfactory kind; it may be the beginning of knowledge, but you have scarcely in your thoughts advanced to the state of Science, whatever the matter may be.

Lord Kelvin

El moviment és el canvi de posició d’un objecte amb el temps. L’estudi del moviment és un dels objectius fonamentals de la física. Les preguntes que ens fem són: Per què es mouen les coses? i com es mouen? A la primera qüestió intentarem donar resposta en la pròxima unitat L’univers mecànic. En aquesta unitat intentarem endinsar-nos en la segona qüestió per a donar una descripció matemàtica del moviment sense preocupar-nos de les causes que l’originen.

Modelització del moviment

La física es dedica a fer models de la realitat, és a dir, es pretén descriure la realitat amb la major precisió i fidelitat possible però, com això és massa complicat perquè la realitat és molt complexa, ens dediquem a fer descripcions més senzilles que preservin els aspectes més importants de la realitat que volem descriure passant per alt altres aspectes que es considerin secundaris, això s’anomena fer un model de la realitat. Per exemple, si volem descriure el moviment d’un cotxe que viatja de Barcelona a Lleida resulta raonable considerar el cotxe com si fos un punt, ja que les seves dimensions no juguen un paper rellevant en la descripció del moviment. En canvi, si el que volem es descriure el moviment d’un cotxe quan aparca, no resulta realista considerar el cotxe com si fos puntual. L’abast d’un model sempre depèn d’això que es vol estudiar, en el nostre cas generalment considerarem situacions on gairebé sempre el mòbil es podrà considerar com un punt. Aquesta aproximació per a descriure el moviment es coneix com cinemàtica del punt material.

Quan diem que volem fer un model per al moviment dels cosos ens estem referint a que volem donar una descripció matemàtica que ens permeti no només descriure com s’ha mogut un cos en el passat sinó que també volem que el nostre model ens permeti predir quina serà l’evolució d’aquest moviment en el futur. Per a fer una descripció matemàtica del moviment hem de definir magnituds que ens puguin dir on es troba en un moment determinat i també hem de dir de quina manera es relacionen aquestes magnituds. Per a descriure el moviment definirem la magnitud posició, que en el Sistema Internacional d’unitats (SI), es mesura en metres i ens dona informació d’on es troba el mòbil¹. Per descriure l’evolució de la posició hem de definir una altra magnitud: el temps². Estem molt acostumats al concepte de temps i ens sembla intuïtiu, però encara no se sap què és en realitat el temps. Per una banda fem servir el temps per a descriure el moviment i per l’altra no podem mesurar el temps sense que hi hagi moviment, la qual cosa ens porta a un cul-de-sac., que ens permetrà donar un ordre a les posicions del mòbil i juga un paper clau en el concepte de canvi. La unitat de temps en el SI és el segon (s). Els ens matemàtics que ens permeten relacionar magnituds es diuen funcions i a les funcions que ens donen la posició en els diferents instants de temps les anomenarem equacions de moviment.

El moviment és relatiu

Una cosa que hem d’entendre per a començar és que tot a l’univers està en moviment i, per tant, sempre que volem descriure un moviment l’hem de fer dient amb respecte a què s’està movent aquell objecte. Diem en aquest cas que adoptem un sistema de referència. Quan volem descriure el moviment d’un vehicle com un cotxe, normalment adoptem com a sistema de referència la Terra. En canvi, si volem estudiar el moviment dels planetes del sistema solar, encara que podem seguir prenent la Terra com a sistema de referència, la descripció del moviment amb aquesta elecció és més complicada i resulta més senzill adoptar el Sol com a sistema de referència³. De manera que sempre que descrivim un moviment hem de dir respecte a quin sistema de referència ho fem. De totes maneres moltes vegades el sistema de referència està sobreentès i no cal dir-ho explícitament. El caràcter relatiu de la posició sembla bastant clara, en canvi el temps des de sempre s’ha considerat com una magnitud absoluta, es a dir el temps passa igual per a tots els observadors. Això és cert si els observadors estan en repòs relatiu o la seva velocitat és petita comparada amb la de la llum al buit, la qual cosa es pot aplicar a qualsevol objecte quotidià com ser un cotxe, un avió i fins i tot un coet espacial amb la tecnologia actual. En aquesta unitat sempre considerarem al temps com una magnitud absoluta.⁴

Moviment unidimensional

Vivim en un univers tridimensional i el moviment, en general, es realitzarà a l’espai de tres dimensions però, hi ha situacions on les restriccions del moviment fan que es pugui considerar com un moviment en una dimensió. Per exemple, si un moviment es produeix en línia recta (moviment rectilini) només necessitarem un valor numèric (magnitud escalar) per a saber la posició del mòbil (Figura inferior).

Moviment rectilini: el mòbil segueix una línia recta, per a saber la seva posició en tenim prou amb donar un nombre real.

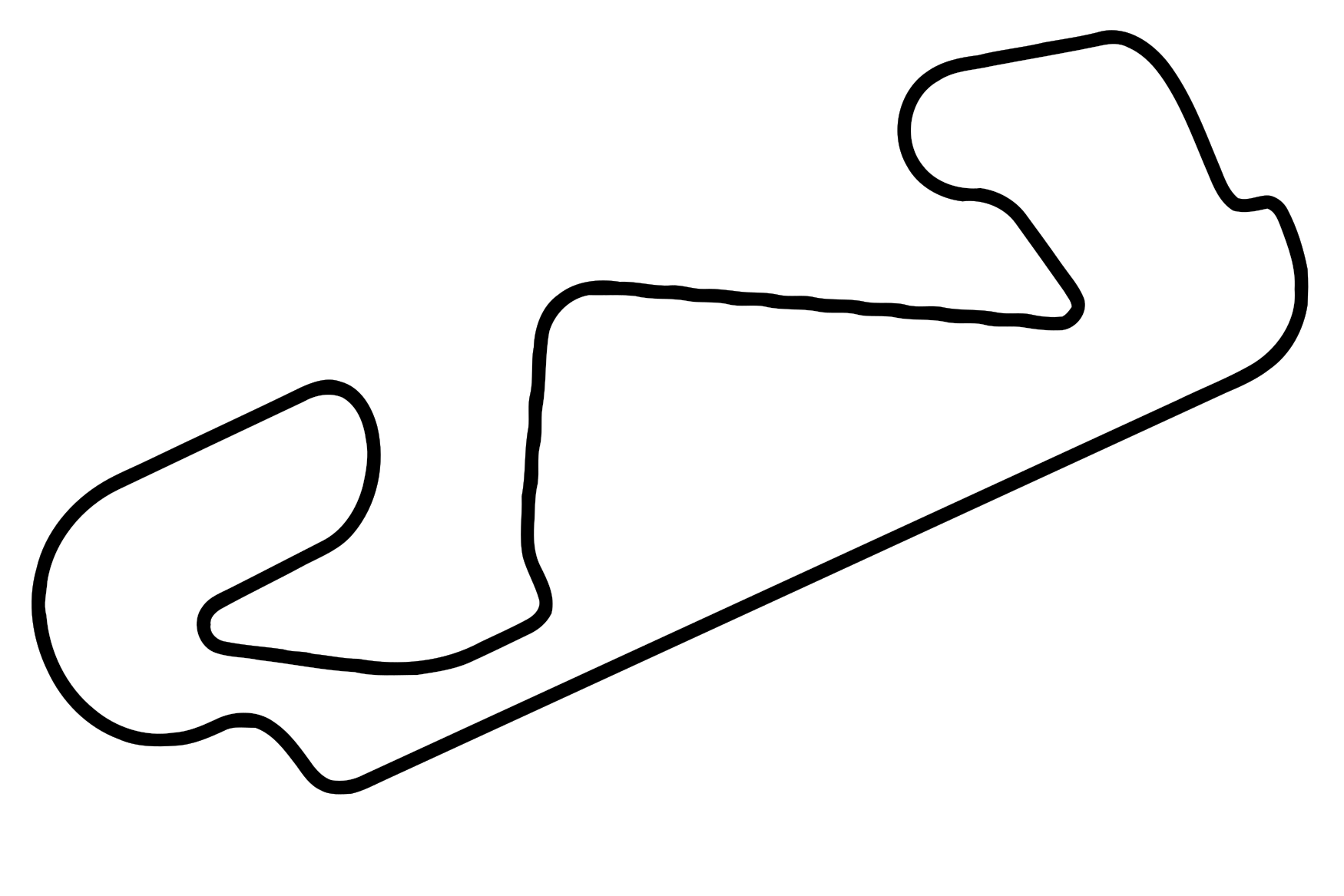
Encara que el moviment no sigui rectilini podríem considerar-lo unidimensional i, per tant, podríem descriure la seva posició amb només un nombre real si coneixem la trajectòria⁵, com és el cas d’un tren o un cotxe que agafa una determinada carretera. A la figura inferior podem veure una vista del circuit de Montmeló, en aquest cas el moviment no és pas rectilini però es pot descriure com un moviment unidimensional, ja que n’hi ha prou amb donar la posició amb un valor numèric com ser \(x=0,7\,\mathrm{km}\) per a saber la seva posició sense ambigüitats, ja que el traçat del circuit marca la trajectòria del mòbil.

Circuit de Montmeló. Quan un cos es mou sobre un camí definit, la seva trajectòria ve donada i només cal donar un valor numèric per a saber exactament la seva posició.

Desplaçament

Anomenarem desplaçament a la diferència entre la posició final \(x\) i la posició inicial \(x_{0}\) del mòbil o, equivalentment, a l’increment de la seva posició. Matemàticament: \(\Delta x=x-x_{0}\)

El desplaçament, a l’igual que la posició, es mesura en metres en el SI i pot tenir signe positiu o negatiu depenent del sentit en que el mòbil es desplaci.

Instants de temps i lapses de temps

Volem estudiar com canvia la posició del mòbil amb el transcurs del temps, per això és necessari mesurar el temps i, per aquest motiu, necessitem definir un instant de referència, origen de temps, instant inicial o instant zero. Per exemple, quan diem que comencem les classes a les 8, estem prenent com origen del temps la mitjanit. Si Messi fa un gol al minut 24 vol dir que s’agafa com minut zero l’instant en que va començar el partit. Als instants de temps anteriors a l’instant zero els assignarem valors negatius.

Anomenarem interval de temps o lapse de temps al temps comprés entre dos instants. L’interval de temps entre un instant inicial \(t_{0}\) i un instant final t serà \(\Delta t=t-t_{0}\). A diferència dels intervals de temps que poden ser positius o negatius, els intervals de temps sempre seran positius, ja que el temps sempre transcorre en un sentit (no podem anar enrere en el temps), per tant \(\Delta t\geq0\).

Velocitat

Volem estudiar l’evolució de la posició d’un mòbil amb el temps i per això necessitem saber com es produeix aquest canvi. Diem que un mòbil que canvia la seva posició molt sovint té més velocitat que un altre que ho fa més a poc a poc. La velocitat ens dóna, doncs, una idea del canvi de la posició amb el temps. Però com fer una definició quantitativa de la velocitat? Per a contestar aquesta qüestió començarem per fer una primera definició, la de velocitat mitjana. La velocitat mitjana \(v_{m}\) entre dos instants de temps \(t_{0}\) i \(t\) serà el quocient entre el desplaçament \((\Delta x)\) i l’interval de temps emprat \((\Delta t=t-t_{0})\):

\[v_{m}=\frac{x-x_{0}}{t-t_{0}}\]

La velocitat es mesura en m/s en el SI però també s’utilitzen altres unitats com km/h. Observem que la velocitat mitjana només té en compte la posició final i inicial del mòbil i no considera les posicions intermèdies per les que passa el mòbil. D’aquesta manera, si el mòbil torna al punt de partida tindrem una velocitat mitjana igual a zero, la qual cosa no vol dir que el mòbil no s’hagi mogut.

Ens podem preguntar si podem tenir una definició de velocitat en un instant en comptes d’un interval de temps, en aquest cas parlaríem de velocitat instantània. Si per exemple volem saber la velocitat \(v_{1}\) que té el mòbil a l’instant \(t_{1}\) quan es troba a la posició \(x_{1}\), podem aprofitar la definició de velocitat mitjana però agafar un interval de temps molt petit, es a dir

\[v_{1}=\frac{x-x_{1}}{t-t_{1}}\]

on \(t\) és un instant molt proper a \(t_{1}\). Quan en física diem “molt proper” volem dir que l’interval \(t-t_{1}\) és de l’ordre de l’error que cometem al fer la mesura del temps (més petit no té sentit).

Acceleració

De la mateixa manera que quan ens vam preguntar com canvia la posició d’un mòbil en el temps hem definit la velocitat, també ens podem preguntar com canvia la velocitat en el temps i ens podem respondre definint una nova magnitud: l’acceleració. Seguint la mateixa metodologia que hem aplicat fins ara podem definir l’acceleració mitjana com

\[a_{m}=\frac{v-v_{0}}{t-t_{0}}\]

L’acceleració instantània serà aleshores igual a l’acceleració mitjana en un interval de temps prou petit.

Moviment Rectilini Uniforme

Quan la velocitat instantània es manté constant a mesura que passa el temps diem que el mòbil té un moviment uniforme. La velocitat instantània es pot escriure

\[\begin{equation}\label{eq:vel_inst} v=\frac{x-x_{0}}{t-t_{0}} \end{equation}\]

on \(x_{0}\) és la posició del mòbil a l’instant \(t_{0}\). Aquesta última relació es pot escriure per a la velocitat instantània perquè la velocitat instantània és constant i aleshores té la mateixa expressió que la velocitat mitjana, per tant en aquest cas no necessitem que l’instant \(t\) sigui proper a \(t_{0}\).

De l’expressió anterior podem aïllar la posició per a obtenir

\[\begin{equation}\label{eq:pos_mru} x=x_{0}+v(t-t_{0}) \end{equation}\]

Aquesta expressió és l’equació de moviment o equació horària del Moviment Rectilini Uniforme (MRU) i ens dóna la posició del mòbil en funció del temps. Aquesta equació correspon a una recta i té tres paràmetres constants que determinen completament el moviment, la velocitat \(v\) i les condicions inicials \(t_{0}\) i \(x_{0}\).

Gràfiques de velocitat i posició

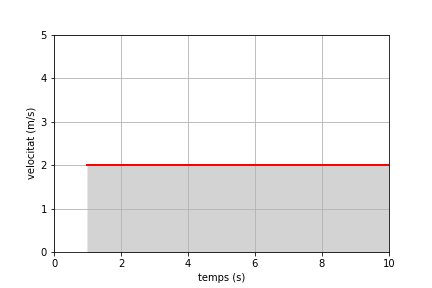
Per veure com són les gràfiques del MRU considerem un exemple. Considerem un mòbil que parteix amb velocitat \(v=2\,\mathrm{m/s}\) en l’instant \(t_{0}=1\,\mathrm{s}\) des de la posició \(x_{0}=5\,\mathrm{m}\) i es mou fins a l’instant \(t=10\,\mathrm{s}\). La figura inferior mostra la gràfica de velocitat en funció del temps per aquest moviment. Podem observar que la gràfica és una recta horitzontal que comença a l’instant inicial i pren el valor de la velocitat. Una observació important és que l’àrea sota la gràfica, que apareix ombrejada a la figura, representa el desplaçament del mòbil entre els instants \(t_{0}=1\,\mathrm{s}\) i \(t=10\,\mathrm{s}\). En aquest cas el desplaçament és \(\Delta x=2(10-1)=18\,\mathrm{m}\).

Gràfica de velocitat en funció del temps (en vermell). L'àrea sota la gràfica, que apareix ombrejada, representa el desplaçament del mòbil entre els instants \(t_{0}=1\,\mathrm{s}\) i \(t=10\,\mathrm{s}\).

La gràfica de posició en funció del temps es pot obtenir a partir de l’equació de moviment

\[x=5+2(t-1)\]

i correspon a una recta que passa pels punts (1 s, 5 m) i (6 s, 15 m) com es pot observar a la gràfica de la figura inferior. També podem comprovar que entre els instants 1s i 10 s el desplaçament és de 18 m com vam obtenir d’analitzar l’àrea de la gràfica de velocitat.

Gràfica de posició en funció del temps. En aquest cas la interpretació gràfica del pendent correspon a la velocitat del mòbil.

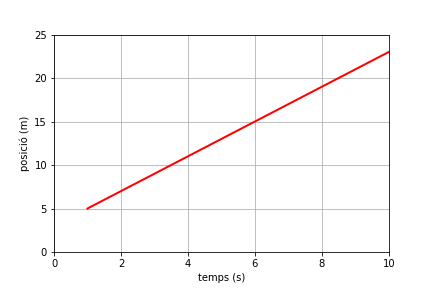
En les gràfiques de posició en funció del temps, el pendent de la gràfica correspon a la velocitat instantània. En aquest cas tenim la gràfica d’una recta i podem determinar el seu pendent prenent qualsevol parell de punts de la recta, com ser (1 s, 5 m) i (6 s, 15 m) i fent el càlcul obtenim que el pendent és

\[v=\frac{x_{1}-x_{0}}{t_{1}-t_{0}}=\frac{15-5}{6-1}=\frac{10}{5}=2\,\mathrm{m/s}\]

Moviment Uniformement Accelerat

Si la velocitat no és constant però varia de manera que l’acceleració instantània sí que ho és tenim un Moviment Uniformement Accelerat (MRUA). Com l’acceleració és constant, l’acceleració instantània serà igual a l’acceleració mitjana i podem escriure

\[a=\frac{v-v_{0}}{t-t_{0}}\]

D’aquesta última última expressió podem obtenir l’equació que ens dóna l’evolució de la velocitat amb el temps:

\[\begin{equation}\label{eq:vel_mrua} v=v_{0}+a(t-t_{0}) \end{equation}\]

La relació anterior presenta la mateixa forma funcional que l’equació de moviment en el MRU, per tant, la velocitat en el MRUA és una recta de pendent igual a l’acceleració i que passa pel punt \((t_{0},v_{0})\).

Com sabem que l’àrea sota la gràfica de velocitat-temps ens dóna el desplaçament del mòbil, intentarem deduir l’equació de moviment del MRUA a partir del càlcul de l’àrea ombrejada en la figura inferior.

Gràfica velocitat-temps del MRUA. L'àrea ombrejada és igual al desplaçament.

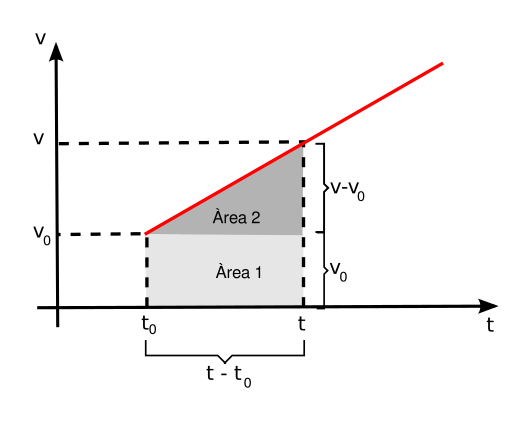
El desplaçament serà d’aquesta manera:

\[x-x_{0}=\mathrm{\grave{A}rea}\,1+\mathrm{\grave{A}rea\,2}\] \[x-x_{0}=v_{0}(t-t_{0})+\frac{(v-v_{0})(t-t_{0})}{2}\]

però, com \(v-v_{0}=a(t-t_{0})\) degut a l’equació de velocitat-temps , la relació anterior es transforma en:

\[\begin{equation}\label{eq:pos_mrua} x=x_{0}+v_{0}(t-t_{0})+\frac{1}{2}a\big(t-t_{0}\big)^{2} \end{equation}\]

que és l’equació de moviment del MRUA on el mòbil té una posició \(x_{0}\) i una velocitat \(v_{0}\) en el instant \(t_{0}\) (coneguts com condicions inicials) i porta una acceleració constant a. Aquests últims quatre paràmetres constants determinen totalment el moviment. Podem observar que es tracta d’una funció de segon grau i, per tant, la gràfica de posició en funció del temps serà una paràbola.

Per veure les gràfiques podem analitzar un exemple. Analitzarem per exemple un mòbil que parteix en l’instant \(t_{0}=0\) de la posició \(x_{0}=10\,\mathrm{m}\) i velocitat inicial \(v_{0}=5\,\mathrm{m/s}\) amb acceleració \(a=1\,\mathrm{m/s^{2}}\). Les equacions de velocitat i posició en funció del temps són:

\[v=5+t\] \[\begin{equation}\label{eq:mov_mrua1} x=10+5t+0,5t^{2} \end{equation}\]

La figura inferior mostra l’evolució de la velocitat durant 10 segons. Si calculem el pendent de la recta obtindrem l’acceleració del moviment. Com la recta té un pendent constant podem calcular el pendent agafant qualsevol parell de punts que pertanyin a la recta. Per exemple, si prenem l’instant inicial i el final tenim els punts (0,5) i (10,15) i el pendent serà

\[a=\frac{v_{f}-v_{0}}{t_{f}-t_{0}}=\frac{15-5}{10-0}=1\,\mathrm{m/s^{2}}\]

Gràfica de velocitat d'un MRUA.

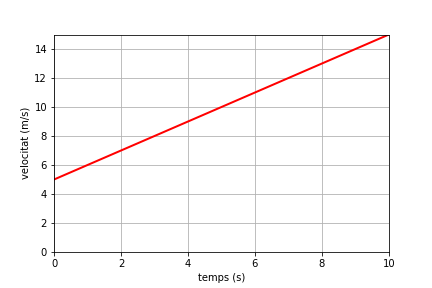
Una altra dada que podem extreure de la gràfica de la figura superior és el desplaçament. Sabem que l’àrea sota la recta representa el desplaçament, per tant

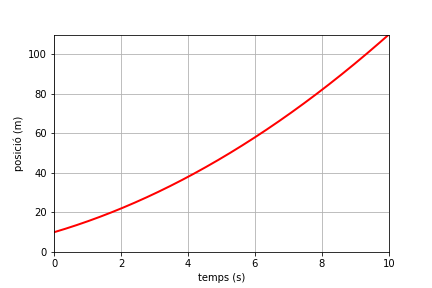
\[\Delta x=(v_{f}-v_{0})(t-t_{0})\] \[\Delta x = (15-5)(10-0)=100\,\mathrm{m}\]

La gràfica de posició en funció del temps la podem traçar a partir d’una taula de valors que podem obtenir de l’equació de moviment . També la podem traçar de manera qualitativa si tenim en compte que és una paràbola, que coneixem dos punts de la gràfica, el punt inicial (0, 10 m) i el final que hem calculat de la gràfica anterior (10 s, 110 m)⁶. També sabem que l’acceleració és positiva, per tant, el pendent (que representa la velocitat) ha d’anar pujant (la gràfica és còncava cap amunt). La figura inferior mostra la gràfica de posició-temps.

Gràfica de posició en funció del temps per un MRUA.

Caiguda lliure

Quan deixem lliure un cos aquest cau per l’acció de l’atracció gravitatòria. L’experiència quotidiana ens diu que no tots els objectes cauen amb la mateixa acceleració, si deixem caure un full de paper estès i un altre full fet una pilota podríem apreciar que el primer cau més lent. Això és degut a que no només hi ha l’acció de la gravetat, sinó que també hi ha l’acció de l’aire que envolta els objectes que produeix una resistència al moviment dels cosos. Hi ha cosos per als quals aquesta resistència es pot negligir. Galileu va ser el primer en adonar-se que tots els cosos caurien amb la mateixa acceleració si no for per la resistència de l’aire, hi ha un experiment que s’ha fet famós on Galileu deixa caure dues peces d’igual mida però de pesos diferents des de la torre de Pisa per a comprovar que queien amb la mateixa acceleració i arribaven al terra al mateix temps. Un experiment equivalent va fer un astronauta de la missió Apol·lo XV va deixar caure un martell i una ploma al mateix temps i va comprovar que arribaven a la superfície de la lluna al mateix temps degut a l’absència d’atmosfera a la superfície de la Lluna.⁷

El físic anglès Brian Cox fa l'experiment de llançar una bola i unes plomes en una cambra de buit per a comprovar que cauen amb la mateixa acceleració

Ja sabem que, si podem negligir l’efecte del fregament de l’aire, l’acceleració de la gravetat és la mateixa per a tots els cosos, però aquesta acceleració no és pas constant sinó que depèn de la distància a la que estem del centre de la Terra. Si tractem d’estudiar la caiguda d’objectes quotidians com una pedra a nivell del mar podem considerar l’acceleració de la gravetat com constant i amb un valor proper a

\[g=9,81\,\mathrm{m/s^{2}}\]

Però, si volem estudiar l’efecte de la gravetat sobre míssils intercontinentals ja no podríem considerar l’acceleració de la gravetat com constant. Tot depèn del que volem estudiar.

Nosaltres tractarem en aquesta unitat sempre problemes on l’acceleració de la gravetat és constant i, per tant, estarem dintre d’un tipus de moviment que ja coneixem bé, el MRUA. Tot el que hem estudiat sobre aquest moviment s’aplica al cas del llançament vertical i caiguda lliure amb l’afegit de que l’acceleració és un valor conegut i val \(9,81\,\mathrm{m/s^{2}}\) en cas d’estar sobre la superfície de la Terra.⁸

Les equacions de velocitat i moviment quedaran respectivament:

\[v=v_{0}+g(t-t_{0})\] \[y=y_{0}+v_{0}(t-t_{0})+\frac{1}{2}g(t-t_{0})^{2}\]

Per a indicar la posició quan tenim un moviment vertical farem servir la lletra y en comptes de x que la utilitzarem per a les coordenades de posició horitzontal.

Moviment relatiu en una dimensió

Fins ara sempre hem observat el moviment des d’un únic punt de vista, el de l’observador generalment fix a la Terra i que generalment anomenarem “sistema de laboratori”. Pot semblar que això és completament natural però pot passar que hi hagi un altre observador en moviment respecte al primer, observant el mateix fenomen. Com serà la descripció del moviment fet per l’observador en moviment? Quina relació hi haurà entre una descripció i l’altra? Com podrem passar d’una a l’altre? Intentarem respondre aquestes qüestions en aquesta secció estudiant el cas més senzill de moviment, on l’observador que es mou ho fa en la mateixa direcció (encara que poden tenir sentits oposats) que el cos sota estudi.

Imaginem una persona que observa el pas d’un tren des de l’andana d’una estació (aquest serà el nostre sistema de coordenades de laboratori i l’indicarem amb la lletra S) i, per l’altra banda, tenim una persona asseguda al tren que serà el nostre sistema mòbil, que indicarem amb la lletra S’ i que es mou amb una velocitat \(v_{0}\) (velocitat del tren) respecte de l’andana. Tant la persona a l’andana com la persona sobre el tren observen el moviment d’una tercera persona (cos del que volem estudiar el seu moviment) caminant pel passadís del tren. Si l’observador S’ veu a la persona caminant amb una velocitat v’ ens preguntem amb quina velocitat el veurà la persona de l’andana.

La manera més natural d’entendre el problema és pensar que la persona de l’andana veurà a la persona que es mou sobre el tren a una velocitat més gran si es mou en el mateix sentit del tren o més petita si es mou en sentit contrari. Això el podríem escriure amb una única relació

\[\begin{equation}\label{eq:relatiu_1} v=v^{,}+v_{0} \end{equation}\]

on \(v\) és la velocitat de la persona caminant vista pel sistema S (andana) , \(v^{,}\) és la velocitat de la persona observada pel sistema S’, mentre que \(v_{0}\) és la velocitat relativa entre el sistema S i el S’. L’equació anterior ens dona la relació de transformació de velocitat que ens permet passar d’un sistema a l’altre.

Nosaltres considerarem sempre sistemes de referència que es mouen amb una velocitat \(v_{0}\) relativa constant. Si la persona que es mou sobre el tren ho fa amb MRU la descripció de l’equació de moviment donada per a cada observador serà

\[x^{,}=x_{0}^{,}+v^{,}(t-t_{0}^{,})\]

i

\[x=x_{0}+v(t-t_{0})\]

Si considerem el mateix instant inicial per a tots dos sistemes de referència i que els orígens dels dos sistemes de referència coincideixen en l’instant inicial obtenim que la posició del mòbil vist pels dos observadors estan relacionats per l’equació

\[\begin{equation}\label{eq:relatiu_2} x=x^{,}+v_{0}t \end{equation}\]

Per altra banda tenim que \(t^{,}=t\), la qual cosa vol dir que el temps transcorre igual per a tots dos observadors. Aquesta última relació juntament amb les equacions de transformació de velocitat i posició es coneixen com transformacions de Galileu del moviment relatiu.⁹

Moviment en dues dimensions

Moviment relatiu en dues dimensions

Començarem l’estudi del moviment en dues dimensions considerant el cas de sistemes de referència que es mouen en direccions perpendiculars entre sí i a velocitat constant. Suposarem que el mòbil es mou en la direcció de l’eix Y’ amb un moviment uniforme i que el sistema S’ es mou en la direcció de l’eix X. Per simplificar el tractament matemàtic podem fer coincidir els orígens dels sistemes de referència S i S’ en l’instant inicial. Tal com l’hem plantejada, en l’instant inicial la situació és com la que veiem a la figura inferior.

Els origen de coordenades i els eixos dels dos sistemes en moviment relatiu coincideixen en l'instant inicial.

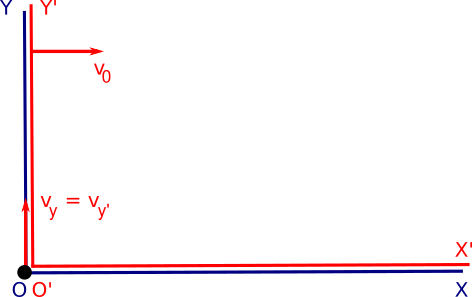
La posició del mòbil observada pel sistema S’ ve donada pel sistema

\[\begin{cases} x^{,}=0\\ y^{,}=v^{,}\Delta t \end{cases}\]

En canvi, des del punt de vista de l’observador del sistema S les equacions resulten més complicades, ja que el mòbil no es desplaça coincidint amb la direcció d’un dels seus eixos. En el temps \(\Delta t\) el mòbil s’haurà desplaçat una distància \(\Delta r=v\Delta t\), com es pot veure a la figura inferior.

Transcorregut un temps \(\Delta t\) els eixos Y i Y' s'ha separat una distància \(x=v_{0}\Delta t\) i el mòbil s'ha desplaçat una distància \(\Delta r=v\Delta t\).

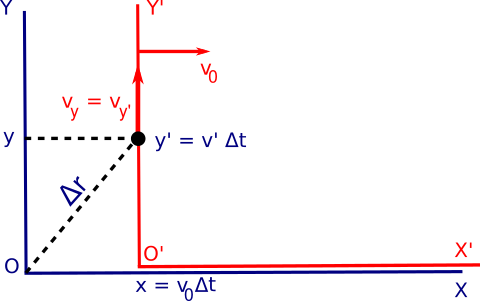
Les equacions de posició del mòbil respecte al sistema S quedaran:

\[\begin{cases} x=v_{0}\Delta t\\ y=y^{,}=v^{,}\Delta t \end{cases}\]

Podem escriure l’equació de la trajectòria (rectilínia) vista pel observador del sistema S

\[\begin{cases} x=v_{0}\Delta t & \Rightarrow\Delta t=\frac{x}{v_{0}}\\ y=v^{,}\Delta t=v^{,}\frac{x}{v_{0}} & \Rightarrow y=\frac{v^{,}}{v_{0}}x \end{cases}\]

Aquesta última equació descriu la trajectòria del mòbil des del punt de vista del sistema S:

\[y=\frac{v^{,}}{v_{0}}x\]

que és l’equació d’una recta amb pendent

\[m=\frac{v^{,}}{v_{0}}\]

El desplaçament del mòbil vist pel sistema S’ serà

\[\Delta y=v^{,}\Delta t\]

i el desplaçament vist pel sistema S serà

\[\Delta r=\sqrt{x^{2}+y^{2}}=\sqrt{(v_{0}\Delta t)^{2}+(v^{,}\Delta t)^{2}}\] \[\Delta r=\sqrt{(v_{0}^{2}+v^{,2})\Delta t^{2}}=\sqrt{(v_{0}^{2}+v^{,2})}\Delta t\]

i d’aquesta última relació tenim que la velocitat \(v\) vista pel sistema S serà

\[v=\frac{\Delta r}{\Delta t}=\sqrt{(v_{0}^{2}+v^{,2})}\]

Aquesta última expressió relaciona la velocitat en el sistema S amb la velocitat del sistema S’. El valor obtingut sempre serà positiu, ja que es tracta del mòdul de la velocitat. Si volem expressar la velocitat de manera vectorial l’haurem d’escriure

\[\vec{v}=\vec{v_{0}}+\vec{v^{,}}=v_{0}\hat{i}+v^{,}\hat{j}\]

Moviment parabòlic

Quan llancem un objecte formant un angle respecte a l’horitzontal (tir oblic) podem observar que la trajectòria que descriu l’objecte és corbada. Per entendre com podem descriure aquest moviment ens fixarem en el moviment que fa una pilota quan la llancem cap amunt mentre ens movem a velocitat constant sobre un patinet. Tal com es veu a la figura inferior, el noi llença la pilota cap amunt en un moviment vertical sota el seu punt de vista, ja que ell sempre veu la pilota a sobre de la seva mà. Però per a un observador que està fix a terra la trajectòria que descriu la pilota es ben altra, és una trajectòria corba resultant de la composició de dos moviments: un moviment uniforme en la direcció horitzontal i un moviment uniformement accelerat en la direcció vertical degut a l’acció de l’acceleració de la gravetat.

Trajectòria d'una pilota quan la llancem verticalment mentre anem muntats a sobre d'un patinet que marxa a velocitat constant. veiem que un observador que està fix a terra veu la trajectòria de la pilota com una corba, mentre que el noi que va sobre el patinet ve en moviment com un tir vertical i caiguda lliure, ja que per al noi la pilota canvia la seva altura però no es desplaça horitzontalment i la pilota sempre està a sobre de la seva mà.

Aquest fenomen ens permet comprendre com descriure un moviment de llançament oblic. El descriurem com un moviment bidimensional amb una acceleració constant que actua només en la direcció vertical.

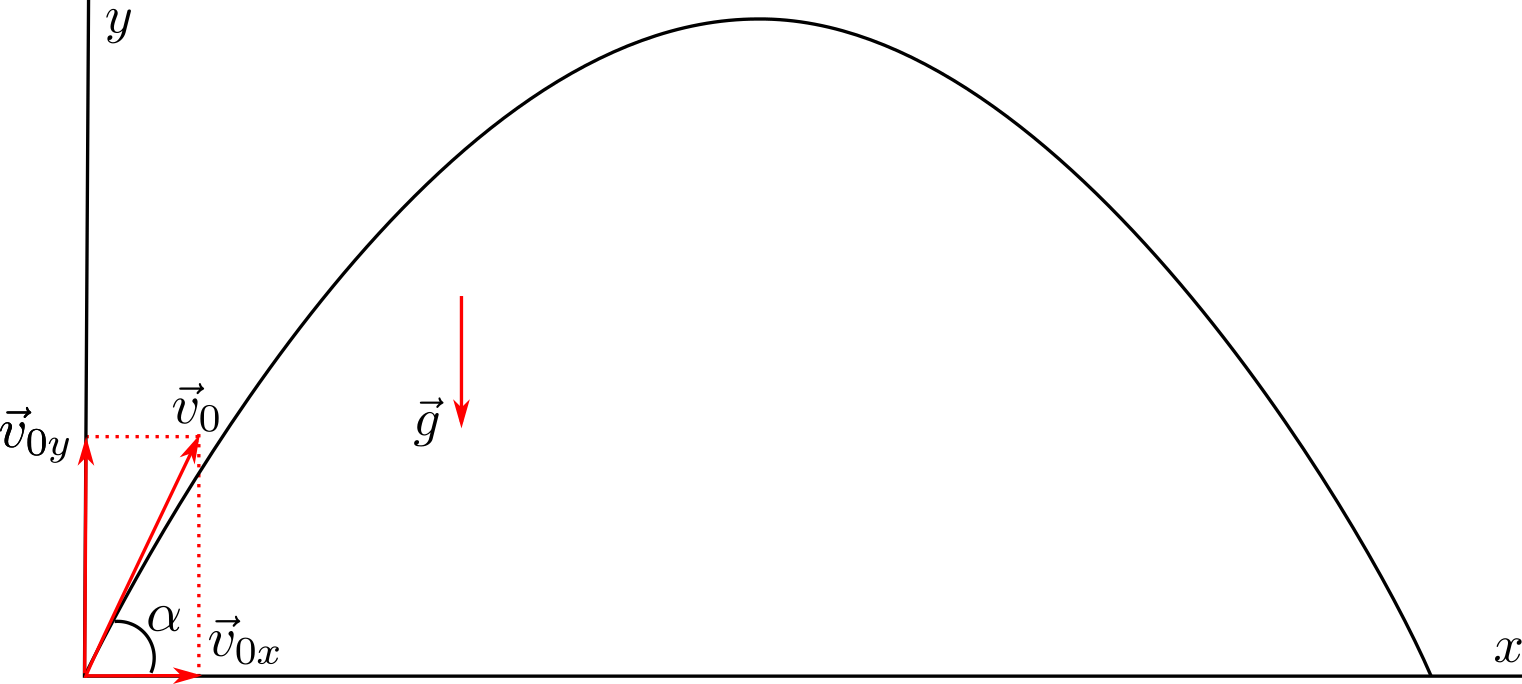
Si llancem un cos amb una velocitat inicial \(\vec{v}_{0}\) formant un angle \(\alpha\) amb l’horitzontal com es veu a la Figura , el cos descriurà un moviment curvilini que podem descriure com la composició d’un moviment horitzontal de velocitat constant

\[v_{0x}=v_{0}\cos\alpha\]

i un altre vertical amb acceleració constant \(g\) i velocitat inicial

\[v_{0y}=v_{0}\sin\alpha\]

Tir oblic. El cos descriu una trajectòria curvilínia que podem pensar com la composició de dos moviments perpendiculars diferents: l'horitzontal de velocitat constant \\(v_{0x}\\) i el vertical de velocitat inicial \\(v_{0y}\\) i acceleració constant \\(g\\).

D’aquesta manera la velocitat del mòbil en qualsevol instant de temps es pot escriure

\[\begin{equation}\label{eq:eq_vel} \begin{cases} v_{x}=v_{0x}\\ v_{y}=v_{0y}+g\big(t-t_{0}\big) \end{cases} \end{equation}\]

o de manera més compacta com a vector:

\[\vec{v}=v_{0x}\hat{\mathrm{i}}+\big(v_{0y}+g\big(t-t_{0}\big)\big)\hat{\mathrm{j}}\]

I l’equació de moviment,

\[\begin{equation}\label{eq:eq_pos} \begin{cases} x=x_{0}+v_{0x}\big(t-t_{0})\\ y=y_{0}+v_{0y}\big(t-t_{0}\big)+\frac{1}{2}g\big(t-t_{0}\big)^{2} \end{cases} \end{equation}\]

o, equivalentment, en forma vectorial

\[\vec{r}=\vec{r}_{0}+\vec{v}_{0}\big(t-t_{0}\big)+\frac{1}{2}\vec{g}\big(t-t_{0}\big)^{2}\]

on

\[\vec{r}=x\mathrm{\hat{i}}+y\hat{\mathrm{j}}\]

és el vector posició,

\[\vec{r}_{0}=x_{0}\mathrm{\hat{i}}+y_{0}\mathrm{\hat{j}}\]

el vector posició inicial,

\[\vec{v}_{0}=v_{0x}\mathrm{\hat{i}}+v_{0y}\mathrm{\hat{j}}\]

el vector velocitat inicial i

\[\vec{g}\]

el vector acceleració de la gravetat, que si estem sobre la superfície de la Terra i considerem com a positiva la direcció vertical cap amunt tindrà un valor \(\vec{g}=-9,8\,\mathrm{m/s^{2}\hat{j}}\).

Les equacions de velocitat i posició contenen tota la informació del moviment i amb elles podrem resoldre gairebé tots els problemes de tir oblic.

Les equacions de posició donen les coordenades de posició en funció del temps, si volem l’equació de la trajectòria, es a dir, l’equació que ens doni com varia l’altura com a funció de la coordenada horitzontal \(y=f(x)\), hem de fer desaparèixer el paràmetre temps de les equacions de moviment. Per a fer-ho aïllarem el temps de la primera de les equacions per a obtenir

\[t-t_{0}=\frac{x-x_{0}}{v_{0x}}\]

i, si ara reemplacem aquest resultat a la segona equació resulta

\[y=y_{0}+v_{0y}\frac{x-x_{0}}{v_{0x}}+\frac{1}{2}g\frac{(x-x_{0})^{2}}{v_{0x}^{2}}\]

que podem reescriure,

\[\begin{equation}\label{eq:traject_parabol} y=y_{0}+\frac{v_{0y}}{v_{0x}}\big(x-x_{0}\big)+\frac{g}{2v_{0x}^{2}}\big(x-x_{0}\big)^{2} \end{equation}\]

on es veu clarament que es tracta de l’equació d’una paràbola. És per això que al tir oblic també se’l coneix com moviment parabòlic. La trajectòria parabòlica es pot apreciar a les figures anteriors. L’equació anterior es coneix com a equació de la trajectòria del moviment parabòlic.

Moviment circular

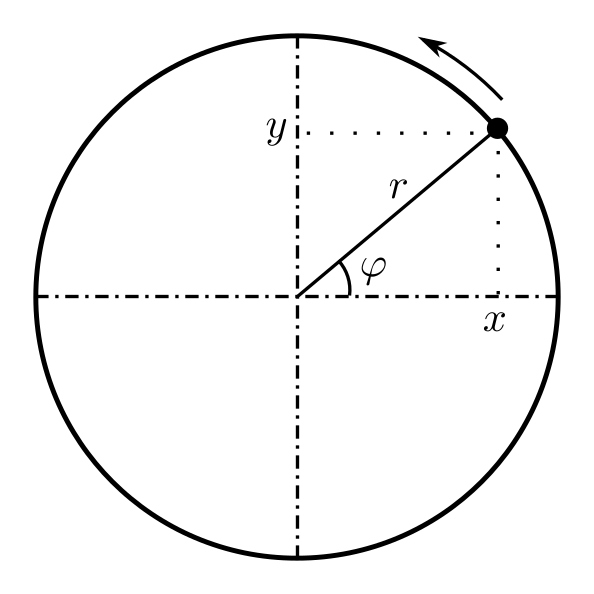
El moviment circular és un moviment que té una circumferència per trajectòria. Podem pensar que es tracta d’un moviment bidimensional perquè es produeix en un pla però en realitat necessitem només una variable per a tenir totalment descrit el moviment. Si sabem el radi de la trajectòria, aleshores ens cal donar només l’angle per a tenir totalment localitzat el mòbil com es pot veure a la figura inferior.

Moviment circular. Les coordenades \(x\) i \(y\) no són pas independents, estan relacionades a través de l'expressió \(r^{2}=x^{2}+y^{2}\), amb la qual cosa només es necessita una quantitat per a tenir completament determinada la posició. En aquest cas el més senzill és fer servir el sistema de coordenades polars, que utilitza com a coordenades el radi \(r\) (constant) i l'angle \(\varphi\) que és l'única variable que necessitem per a tenir completament localitzat el mòbil.

Sistema de coordenades polars

Fins ara hem fet servir sempre sistemes de coordenades cartesianes (rectangulars) però moltes vegades, depenent del problema que volem tractar, convé fer servir sistemes de representació diferents. En el cas del moviment circular el sistema més natural per a treballar és el sistema polar. El sistema polar utilitza la distància a l’objecte i l’angle respecte a l’eix X per a representar la posició d’un objecte i, com en el moviment circular la distància \(r\) (radi) és constant, l’única variable resulta ser l’angle \(\varphi\). Sempre es pot passar d’un sistema a l’altre amb unes regles de transformació senzilles (veure figura anterior). Per a passar de sistema polar a cartesià:

\[\begin{cases} x=r\cos\varphi\\ y=r\sin\varphi \end{cases}\]

i, si volem passar de cartesià a polar:

\[\begin{cases} r=\sqrt{x^{2}+y^{2}}\\ \varphi=\arctan\big(\frac{y}{x}\big) \end{cases}\]

on r es mesura en unitats de longitud (metres al SI) i l’angle el mesurarem en radiants (rad).

El radiant es defineix com el quocient entre l’arc \(s\) i el radi \(r\),

\[\varphi=\frac{s}{r}\]

que resulta independent de la mida de la circumferència. Si agafem un radi més gran, també serà més gran l’arc, de manera que l’apertura seguirà sent la mateixa i és aquesta apertura el que anomenem angle. Amb aquesta definició l’angle no té unitats, ja que tant l’arc com el radi es mesurem amb les mateixes unitats de longitud, però per a indicar que estem aprlant d’angles li direm radiant. ¹⁰

Velocitat angular

De la mateixa manera que vam fer abans quan vam definir la velocitat com a la variació de la posició en el temps, ara podem definir la variació de l’angle en el temps com a velocitat angular. Si considerem un interval de temps \(\Delta t\) i observem un desplaçament angular \(\Delta\varphi\), direm que el mòbil té una velocitat angular mitjana \(\omega_{m}\), tal que,¹¹

\[\begin{equation}\label{eq:omega_m} \omega_{m}=\frac{\Delta\varphi}{\Delta t}=\frac{\varphi-\varphi_{0}}{t-t_{0}} \end{equation}\]

que té unitats de rad/s.

Moviment circular uniforme

Si el moviment circular es realitza amb un ritme constant i sempre tarda el mateix en donar una volta direm que es mou amb un moviment circular uniforme (MCU). Com sempre tarda el mateix en fer un cicle, definirem aquest temps com a període i l’assignarem la lletra \(T\). Per exemple, les manetes del rellotge tenen diferents períodes depenent de què mesurin. l’agulla horària té un període de 12 hores, la agulla minutera té un període d’una hora i la que marca els segons té un període de 60 segons. En el cas del moviment de la terra al voltant del Sol, el període és de 365,25 dies.

Una altra magnitud habitual quan parlem de moviments periòdics en general i circular uniforme en particular, és la freqüència, \(f\), que és la quantitat de cicles o voltes que fa per unitat de temps, així

\[f=\frac{N}{\Delta t}\]

on \(N\) és el nombre de voltes que fa en un interval de temps \(\Delta t\). Les unitats amb que mesurem la freqüència són \(\mathrm{s^{-1}}=\mathrm{Hz}\) els hertz. Si per a calcular la freqüència utilitzem només una volta, el temps emprat és igual al període i aleshores podem escriure

\[\begin{equation}\label{eq:freq} f=\frac{1}{T} \end{equation}\]

Si tenim en compte que en un MCU la velocitat angular és constant, l’expressió per a la velocitat angular mitjana la podem fer servir per a la velocitat angular instantània, ja que coincideixen en aquest cas. Si utilitzem l’expressió de la freqüència per a una volta, l’angle recorregut és \(2\pi\) en un interval de temps igual al període, per tant, obtenim l’expressió que relaciona la velocitat angular amb el període:

\[\begin{equation}\label{eq:freq_ang} \omega=\frac{2\pi}{T} \end{equation}\]

i, si fem servir l’expressió de la freqüència dintre de la freqüència angular, obtenim l’expressió que relaciona la freqüència angular i la freqüència:

\[\omega=2\pi f\]

Utilitzant l’expressió de la freqüència angular mitjana podem escriure l’equació de moviment en la seva versió angular pel MCU:

\[\varphi=\varphi_{0}+\omega\big(t-t_{0}\big)\]

que ens dona l’angle com a funció del temps, sabent l’angle \(\varphi_{0}\) que té el mòbil en l’instant \(t_{0}\) i la velocitat angular.

Si volem conèixer l’arc recorregut només ens cal multiplicar l’angle pel radi, \(r\), de la trajectòria:

\[s=\varphi r=\varphi_{0}r+\omega r\big(t-t_{0}\big)\]

o, equivalentment,

\[s=s_{0}+v\big(t-t_{0}\big)\]

on

\[v=\omega r\]

és la velocitat tangencial, també anomenada velocitat lineal. Hem de dir que aquesta magnitud és constant en un MCU, ja que tant la velocitat angular com el radi de la trajectòria ho són. Però hem de tenir en compte que aquí només ens estem fixant en el mòdul de la velocitat, es a dir, la celeritat o rapidesa, però que la velocitat és en realitat una magnitud vectorial i això té una gran importància quan ens fixem en la variació de la velocitat en el temps, es a dir, el l’acceleració. Podem pensar que el MCU no té acceleració perquè es mou amb velocitat constant, però això seria un gran error. Tal com hem dit la velocitat és una magnitud vectorial que es caracteritza per tenir un mòdul una direcció i un sentit i, per tant, qualsevol d’aquestes característiques que canviï serà un canvi de velocitat i, per tant, tindrà associada una acceleració. Estudiarem amb deteniment aquesta qüestió a la secció següent.

Acceleració d’un moviment circular uniforme

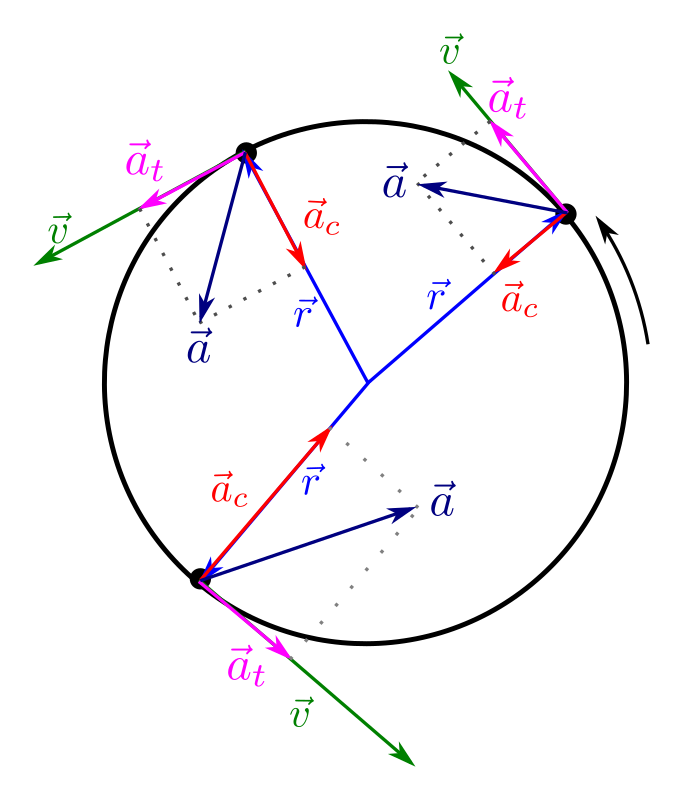
Hem vist que el MCU es caracteritza per tenir el mòdul de la velocitat constant, però el fet d’estar subjecte a una acceleració es deu a un canvi a qualsevol de les característiques vectorials de la velocitat, per tant, un canvi en la direcció de moviment té associat una acceleració. Tractarem de deduir el valor de l’acceleració en un MCU i per a fer-ho ens ajudarem amb la figura següent. Allí veiem un moviment circular uniforme on el mòbil passa de la posició P a la posició Q descrivint un angle \Delta\varphi mentre descriu una trajectòria de radi \(r\) constant en un temps \(\Delta t\).

Acceleració centrípeta

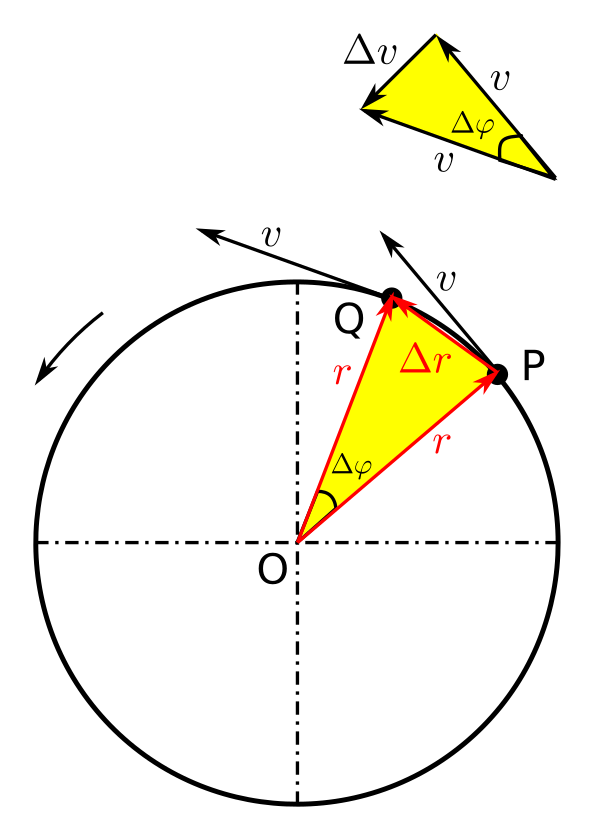
El desplaçament del mòbil en l’interval de temps \(\Delta t\) és \(\Delta r\) i, com la velocitat \(v\) és sempre tangent a la trajectòria, té una direcció sempre perpendicular al radi. Per tant, si analitzem el triangle OPQ (indicat en groc) veiem que és isòsceles i resulta semblant¹² al triangle que s’obté de fer coincidir l’origen dels dos vectors velocitat com es pot veure al detall superior de la figura anterior. Si utilitzem la proporcionalitat dels seus costats podem establir que

\[\frac{\Delta v}{v}=\frac{\Delta r}{r}\]

que podem reescriure com

\[\Delta v=\frac{v}{r}\Delta r\]

i, si dividim ambdós membres per l’interval de temps \(\Delta t\) obtenim

\[\frac{\Delta v}{\Delta t}=\frac{v}{r}\frac{\Delta r}{\Delta t}\]

Però \(\Delta v/\Delta t=a\) i \(\Delta r/\Delta t=v\), per tant podem reescriure l’expressió anterior com¹³

\[a=\frac{v^{2}}{r}\]

Hem obtingut l’expressió de l’acceleració a la que està sotmès un mòbil que es mou seguint un MCU. Aquesta acceleració té la mateixa direcció i sentit que \(\Delta v\) (veure figura anterior), si considerem un interval de temps molt petit podem veure que \(\Delta\varphi\) també serà molt petit i que \Delta v tindrà una direcció perpendicular a la velocitat i, el mateix passa amb l’acceleració. Per tant, l’acceleració tindrà una direcció radial cap endins i, per aquest motiu, se la coneix amb el nom d’acceleració centrípeta o acceleració normal, per ser perpendicular (normal) a la trajectòria.

Sistema de coordenades intrínseques

Ja hem vist que a vegades podem fer servir un sistema de coordenades diferent al cartesià si s’ajusta millor al problema sota estudi. Així hem utilitzat el sistema de coordenades polar per descriure el moviment circular. Un altre sistema de coordenades que resulta d’utilitat per descriure moviments curvilinis és el sistema de coordenades intrínseques¹⁴. En aquest sistema de coordenades els vectors unitaris (versors) que formen la base del pla es mouen amb el mòbil. Un dels versors té la mateixa direcció i el mateix sentit que el vector velocitat i l’anomenarem versor tangencial, \(\mathrm{\hat{t}}\), de manera que

\[\mathrm{\hat{t}}=\frac{\vec{v}}{\left|\vec{v}\right|}\]

i l’altre versor l’anomenarem versor normal, \(\hat{\mathrm{n}}\), i té direcció perpendicular a \(\hat{\mathrm{t}}\), i sentit cap a la part convexa de la trajectòria. A la figura següent es pot veure com van variant els versors intrínsecs a mesura que el mòbil canvia de posició del mòbil.

Sistema de coordenades intrínseques. Els vectors unitaris \(\mathrm{\hat{t}}\) i \(\mathrm{\hat{n}}\) van seguint el mòbil, el primer sempre té direcció tangent a la trajectòria com el vector velocitat i el segon és perpendicular a la trajectòria i sempre apunta en el sentit exterior a la trajectòria.

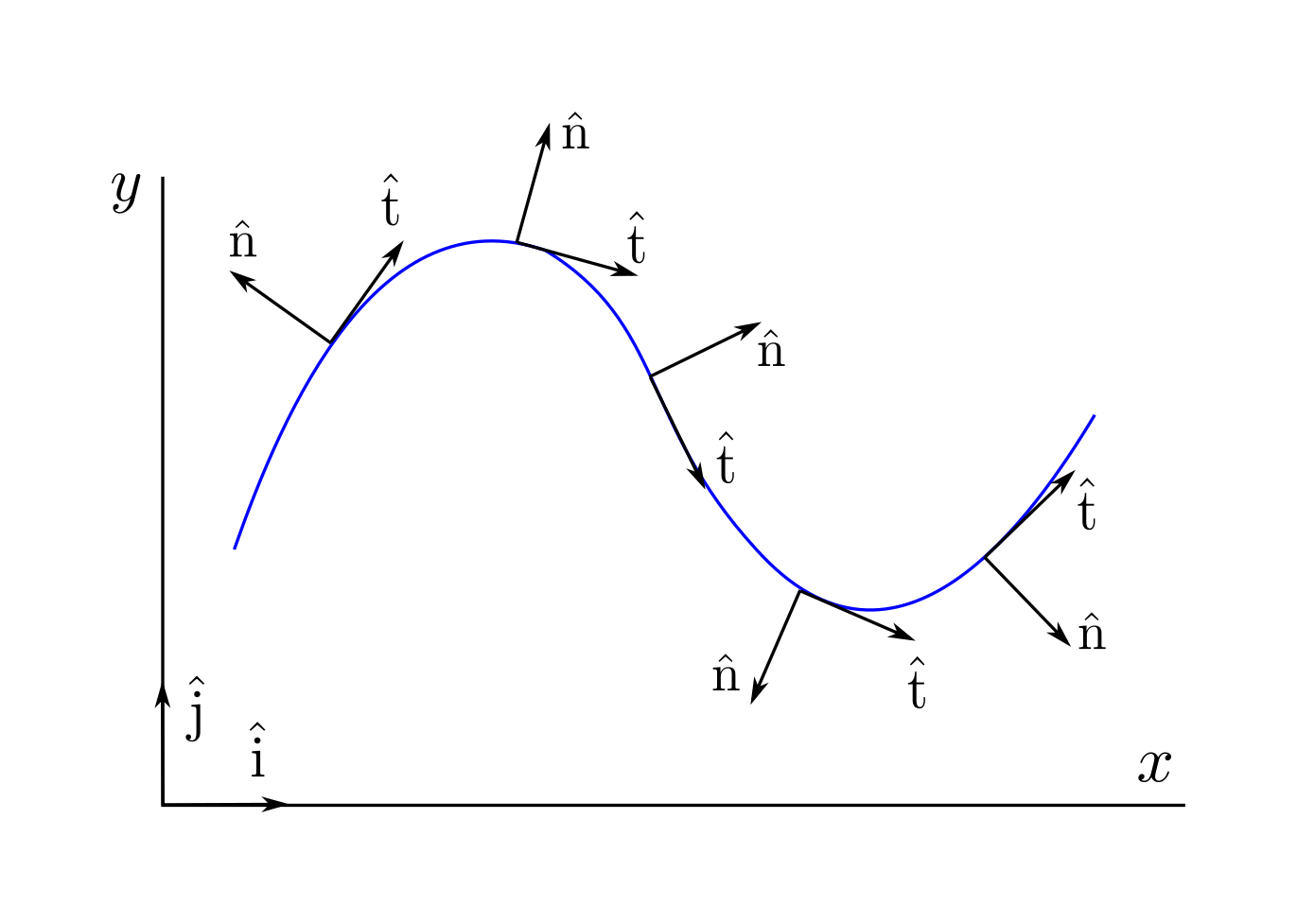
En el cas del moviment circular uniforme podem escriure les magnituds vectorials més rellevants de manera molt senzilla fent servir el sistema de coordenades intrínseques. A la figura es poden veure algunes d’aquestes magnituds. El vector posició (en blau a la figura) s’escriu

\[\vec{r}=r\hat{\mathrm{n}}\]

el vector velocitat (en verd a la figura) s’escriu

\[\vec{v}=v\hat{\mathrm{t}}\]

i l’acceleració centrípeta (en vermell a la figura) s’escriu¹⁵

\[\vec{a_{c}}=-\frac{v^{2}}{r}\hat{\mathrm{n}}\]

Vectors posició, velocitat i acceleració en un MCU. Estan indicats els vectors unitaris intrínsecs.

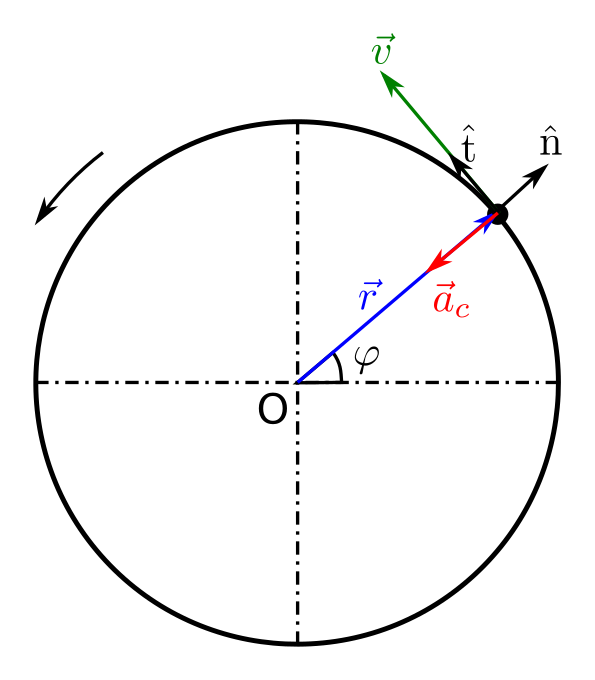
En general una acceleració que sigui tangent a la trajectòria tindrà com a causa el canvi en el mòdul de la velocitat, en canvi una acceleració amb direcció normal tindrà efecte només sobre la direcció del moviment sense afectar el mòdul de la velocitat, com en el cas del MCU.

Moviment circular uniformement accelerat

Si el moviment circular es produeix de manera que la velocitat angular varia direm que es tracta d’un moviment circular no uniforme, essent la seva acceleració angular mitjana en un interval de temps \(\Delta t=t-t_{0}\):

\[\alpha_{m}=\frac{\omega-\omega_{0}}{t-t_{0}}\]

on l’acceleració angular es mesura en radiants partit segon al quadrat (\(\mathrm{rad/s^{2}}\)).

Si el ritme de canvi del mòdul de la velocitat és constant, aleshores l’acceleració angular instantània coincidirà amb l’acceleració mitjana i podríem escriure

\[\begin{equation}\label{eq:omega_mcua} \omega=\omega_{0}+\alpha\big(t-t_{0}\big) \end{equation}\]

que ens dona l’equació de l’evolució de la velocitat en funció del temps per a un moviment circular uniformement accelerat (MCUA). Fent el mateix raonament que vam fer per deduir l’equació de moviment per a un MRUA, es pot demostrar que l’angle en funció del temps per a un MCUA és

\[\begin{equation}\label{eq:eq_mov_mcua} \varphi=\varphi_{0}+\omega_{0}\big(t-t_{0}\big)+\frac{1}{2}\alpha\big(t-t_{0}\big)^{2} \end{equation}\]

Si multipliquem les equacions de \(\omega\) i \(\varphi\) pel radi de la trajectòria podem obtenir les relacions tangencials que donen la velocitat i l’arc

\[v=v_{0}+a_{t}\big(t-t_{0}\big)\]

i

\[s=s_{0}+v_{0}\big(t-t_{0}\big)+\frac{1}{2}a_{t}\big(t-t_{0}\big)^{2}\]

on

\[a_{t}=\alpha r\]

és l’acceleració tangencial causant del canvi en el mòdul de la velocitat. L’acceleració normal o centrípeta mantindrà la mateixa expressió que pel MCU

\[a_{n}=\frac{v^{2}}{r}\]

però hem de tenir en compte que ara ja no té mòdul constant degut a que v varia en el temps. El vector acceleració es pot escriure en el sistema de coordenades intrínseques com

\[\vec{a}=a_{t}\hat{\mathrm{t}}+a_{n}\hat{\mathrm{n}}=\alpha r\hat{\mathrm{t}}-\frac{v^{2}}{r}\hat{\mathrm{n}}\]

i el seu mòdul

\[a=\sqrt{a_{t}^{2}+a_{n}^{2}}\]

Moviment circular uniformement accelerat. Es pot veure com varia el mòdul de la velocitat i també l'acceleració centrípeta i l'acceleració total.

Notes

^{1. En general la posició serà una magnitud vectorialPel futur: aquí s’hauria d’enviar a un apèndix matemàtic on es faci una definició de magnituds vectorials i les seves propietats però, sota determinades condicions es pot escriure de manera més senzilla com un nombre escalar.↩}

^{2. El concepte de temps és motiu de gran discussió entre els físics i filòsofs. Estem molt acostumats al concepte de temps i ens sembla intuïtiu, però encara no se sap què és en realitat el temps. Per una banda fem servir el temps per a descriure el moviment i per l’altra no podem mesurar el temps sense que hi hagi moviment, la qual cosa ens porta a un cul-de-sac.↩}

^{3. Aquesta qüestió forma part d’una de les histories més profundes de l’evolució de la ciència com va ser la revolució copernicana. Fins al segle XVI es va creure sense cap dubte que la Terra estava estàtica al centre de l’univers i que tot girava al seu voltant, aquest sistema geocèntric va ser imposat per Ptolomeu. Aquesta concepció va ser posada en dubta per Nicolau Copèrnic, que va moure el centre de l’univers al Sol i amb això va desencadenar tota una revolució i l’enfrontament de científics com Galileu, Kepler o Giordano Bruno amb l’esglesia catòlica.↩}

^{4. Des de 1905 se sap que el temps i l’espai no són ens separats i que els hem de considerar com una sola cosa, l’espaitemps. D’aquesta manera el temps no és una magnitud absoluta sinó que depèn del sistema de referència considerat però això només resulta rellevant quan la velocitats involucrades no són menyspreables respecte a la velocitat de la llum. ↩}

^{5. La trajectòria d’un mòbil està formada per tots els punts per on passa el mòbil.↩}

^{6. Obervem que la posició final és igual a la posició inicial més el desplaçament \(x_{f}=x_{0}+\Delta x=10+100=110\,\mathrm{m}\)↩}

^{7. Es pot veure el vídeo de l’experiment a YouTube: https://youtu.be/oYEgdZ3iEKA↩}

^{8. Un dels errors més usuals al estudiar els moviments verticals és tractar de manera diferent l’etapa de pujada de l’objecte de l’etapa de caiguda i plantejar equacions diferents en cadascuna d’elles. No és pas necessari fer aquesta distinció, ja que tan de pujada com de baixada el cos està sotmès a la mateixa acceleració, i per tant a les mateixes equacions de moviment. Per tant tot el moviment es pot descriure amb la mateixa equació de moviment.↩}

^{9. Ja veurem que la suposició d’un temps absolut només és vàlida quan els sistemes no es mouen a una gran velocitat relativa, quan el moviment d’un sistema respecte a l’altre no és molt més petit que la velocitat de la llum s’han de fer servir les relacions de transformació d’Einstein de la relativitat especial.↩}

^{10. El radiant és una unitat “fantasma”, ja que la utilitzem com unitat per a una magnitud adimensional, és per aquest motiu que quan apareix alguna unitat multiplicant al radiant aquest desapareix i ja no l’escrivim.↩}

^{11. Per a indicar la velocitat angular farem servir la lletra grega omega minúscula \(\omega\).↩}

^{12. Dos triangles són semblants si tenen els angles iguals i els costats proporcionals.↩}

^{13. Dos triangles són semblants si tenen els angles iguals i els costats proporcionals.↩}

^{14. Intrínsec vol dir propi i es diu així perquè el sistema és propi de cada mòbil.↩}

^{15. Noteu el signe negatiu de l’acceleració per a indicar que té el sentit contrari al del versor↩}